Resonant Systems: multiphonic resonance complexes in sine-wave excited cymbal clusters
This forms part of a larger project of compositional research that treats instruments as resonant spaces, examining how different forces activate and sculpt the natural resonant frequencies of that space, and composing pieces that explore this harmony either systematically or performatively. See also the collection of pieces called There are neither wholes nor parts.
This project examines the compositional possibilities in generating sustained systems of oscillating pitch patterns through the excitation of coupled metal cymbals by variable sinusoidal waves. The physical system requires two or more cymbals mechanically combined to maximise coupling and minimise loss of acoustic energy. Transducers apply sinusoidal waves at high amplitude to drive the cymbals: frequencies of the sinusoidal waves are derived from pre-analysis of the resonant frequencies of the specific cymbals. Compositional variables for the piece include the set of derived frequencies, along with a range of amplitudes that keep the system between silence and the threshold of chaotic vibration.
The compositional interest lies in the audible pattern generation possible through performative exploration of the system, locating frequencies that excite different forms of periodic oscillation, and maintaining amplitude levels near the bifurcation points (see below) of the system to exploit the near-chaotic instability.
In Resonant Systems a single sine-wave drone excites the resonant frequencies of two coupled cymbals, making a network of interacting harmonies. This varies between three typical states, (1) a single pitch with linear harmonics, (2) a multiphonic-like, complex inharmonic sound of several interacting vibrational modes, (3) chaotic vibration, where the energy cascades, activating many modes simultaneously in a noisy spectrum.
In performance, the sound mostly develops in its own time as acoustic energy builds up in the cymbals. Occasionally the performer will 'nudge' the system with very small changes in frequency (generally less than 1-2Hz) or amplitude, to force the system to evolve in a different direction. The performer's goal is to find points where the sound hovers between stable and unstable states, gradually being pulled into a new state. Longer performances will typically explore a few different frequency areas: e.g. 699-721Hz and 1600-1650Hz.
The two cymbals are strongly coupled (through a metal rod) to a transducer (the black object underneath). The transducer is essentially a loudspeaker without a cone, so it doesn't project much sound unless directly connected to a resonating object or surface. Each cymbal has its own resonant frequencies, which have coupling relations with each other. Two or more cymbals increases the complexity and unpredictability of these relationships as the different resonant frequencies and vibrational modes interact with each other, interfering constructively and/or destructively.
Audio
More audio and video recordings will follow in the coming months, for now here are two: This is a recording from June of the cymbals shown above [11mins mp3], I think there's a couple of places here where I tried to use two sine-waves together; and here's an early audio example with only a single cymbal excited by four different frequencies, one after the other. [new] Recording here of a 20min performance from ISSTA convocation at Cork School of Music, August 2012.

One Cymbal and transducer

Two Cymbals and transducer

Detail of coupling
Laser Interferometry Holography
Did some Laser Interferometry Holography with David Bryant at Uni. of Huddersfield to try to capture the vibrational modes of the quasiperiodic "multiphonic" sounds; to try and see if the sounds are caused by interference between different modes of vibration, this is the overall course of research at the moment.
The images here are:
1: reference image of the cymbal vibrating in normal linear fashion. Excited by 120hz sinewave and showing a single stable mode of vibration. The mode appears to be (2,0), two diametral nodes. See here for brief overview of vibrational modes in cymbals/gongs.
2: quasiperiodic vibration excited by 1857hz sinewave. This is a stable multiphonic sound with a complex pattern of vibrational modes. at the end of the audio sample (beneath image) you can hear the sinewave on its own for reference.
3: quasiperiodic vibration excited by 1378hz sinewave. This is a stable multiphonic sound, more complex than 1857hz, and with a similarly complex pattern of vibrational modes though a little less well defined, possibly because of the richer spectrum.
4: chaotic vibration excited by 1857hz sinewave. This is an unstable noisy sound with a very complex pattern of vibrational modes: it's impossible to pick out the modes due to the chaotic vibration, only a some isolated nodes are visible.
Remaining pictures are spectra of the two quasiperiodic vibrations, there's a lot of noise in these recordings especially at the low end, because the laser equipment was running in the background. And finally, a documentation shot of the holography setup: the laser is fired in the dark so no shots of that unfortunately.

120hz excitation, linear response

1857hz excitation, quasiperiodic response
[audio]
1378hz excitation, quasiperiodic response
[audio]
1857hz excitation, chaotic response
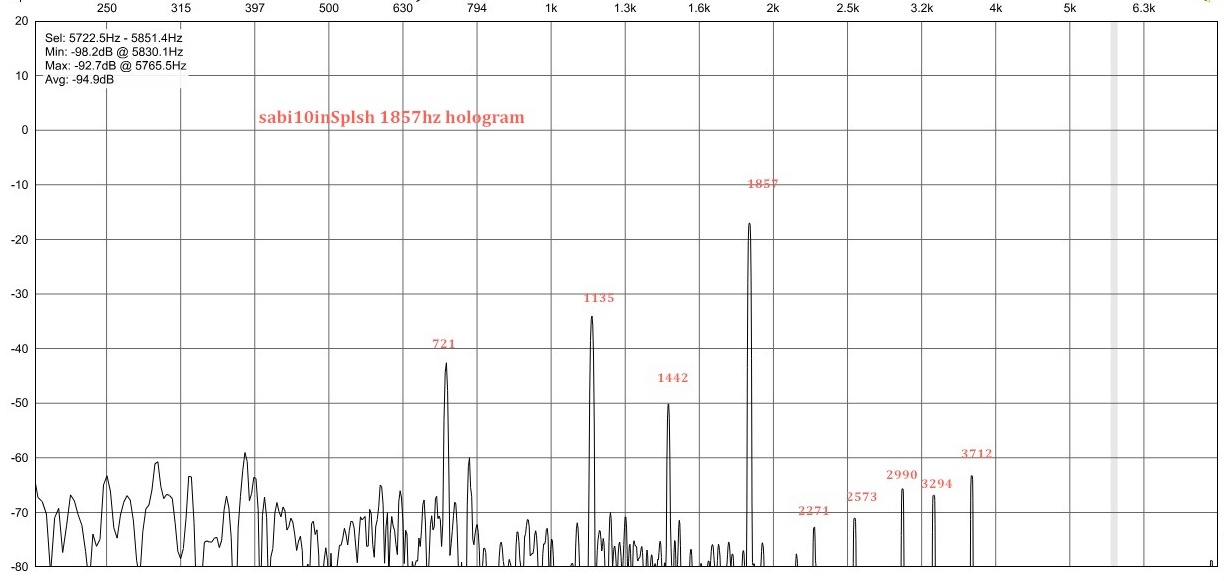
spectrum of 1857hz vibration
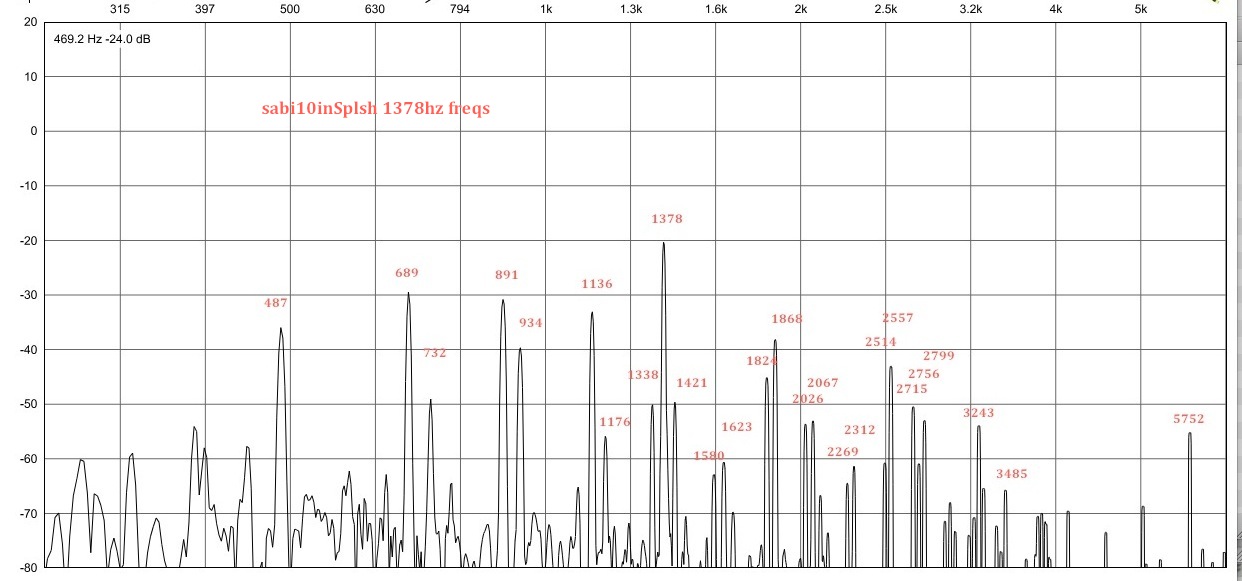
spectrum of 1378hz vibration

holography setup
Development of the project (backstory)
This project came out of a strange series of leaps and connections. It began in a rehearsal with Ann Evans who was playing my piece Nano, and for this she had worked out about 150 fingerings for pitches within a minor third A-C. I dreamt of a piece that could take real advantage of these miniscule pitch variations. So I thought of something that would use sine waves to create beating patterns, the static sine wave would create audible beatings that would change with the different saxophone fingerings, amplifying the differences and making clear the pitch changes that are otherwise almost unnoticeable.
The sine waves would work best if they could be inside the saxophone, interacting with the air column already vibrating from the reed/air-flow. I considered putting a small speaker in the saxophone bell but thought it would be even more effective if the sound was not coming from a separate object (the speaker) but rather seemed to be as much a part of the saxophone as the sax sound itself. This could be achieved by making the saxophone body itself vibrate by using a transducer to excite the saxophone with the sine wave. However, two problems arise here: (1) the transducer would need to be attached mechanically to the saxophone, to maximise the coupling and the transfer of acoustic energy from sine to sax, this would require glueing or even drilling into the instrument to screw the transducer in place; (2) to be loud enough, the transducer would have to be quite large, and thus an unieldy weight to add to a saxophone (though feasible on an instrument that is not supported entirely by the player alone).
Alongside these ideas, the leap to using cymbals came about from connections between several overlapping strands of thought. I had a parallel set of concerns in thinking about how musical instruments can be treated as non-linear dynamical systems, especially with regards to woodwind multiphonics and their inherent non-linearities. I also was thinking of ways to use Alex Harker's impulse-response tools to create convolution reverbs of highly coloured spaces (see my Bowls project that developed around the same time). And I had just acquired a set of broken cymbals that had interesting resonances due to their lop-sidedness. With all of these ideas floating around, I was still thinking of applying sine waves to the saxophone body, but the more I thought about it it seemed that what I should be doing is trying to excite the existing resonances of an object, in the same way that the impulse response sweeps do. I took my cheap maplin transducers and applied sine waves to the broken cymbals I had, the results were disappointing, some hints of resonance but no real amplification, except for a hopeful glimmer around 5000hz where touching the transducer to the bell of the cymbal made a terryfing shrieking sound, resonance I presumed.
The maplin transducers simply didn't have the power to activate the metal of the cymbals. I found (via Eric Maestri) a US company that sold 80W transducers but was reluctant to order until I knew the idea would work. At this point I made contact with the university engineering technicians, who advised me to talk to a colleague in mechanical engineering who was, as it happened, a goldmine. It turns out we had a whole dept here whose main focus was on exciting metal objects (car parts mainly) with sine waves and white noise to find metal fatigue and perform stress testing. They introduced me to the concept of the "shaker", a device designed to vibrate objects at any given frequency and with great force. After knocking on some doors I found a generous engineering researcher who was happy to let me use his new shaker. From there everything fell into place, preliminary tests on some cymbals showed that at high amplitudes the sine waves would excite the resonant frequencies of the cymbal to cascade and excite other related vibrational modes and frequencies, creating a multiphonic effect on the cymbal. I also found that if the amplitude was increased further the cymbal sound would approach the high noise content that we more typically associate with the rolled cymbal effect. I subsequently ordered some 80W transducers and started to experiment.
Chaotic regimes in cymbal acoustics.
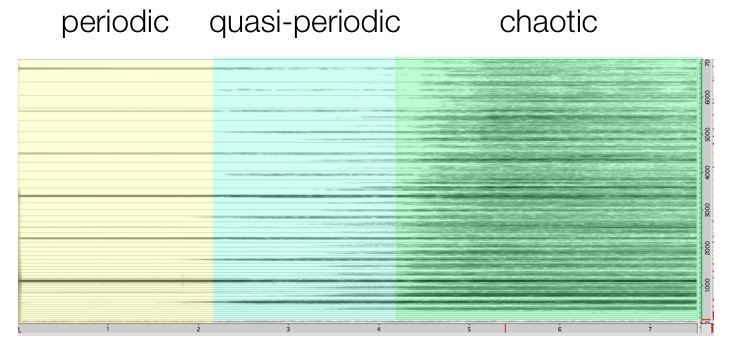
The pitched sound of sheet metal is always audible but often masked, reduced to a colouration of the cymbal, especially as cymbals are mosty used for their noise content. When struck hard with a stick, the cymbal oscillates chaotically, the energy spread over multiple vibrational modes (see here for example of slow-motion cymbal vibration). Even when struck lightly the pitch is not very clear as the cymbals are inharmonic, with many different and unrelated resonant frequencies (or non-integer relations at least). However, when a cymbal is excited by a sine wave the energy is concentrated. When the excitation frequency is also a resonant frequency of the cymbal then the energy is sharply focused on that pitch, and amplified by the cymbal resonance. As the excitation amplitude is increased, the sound has several distinct stages: (1) periodic
, the excitation frequency and some mostly linear/harmonic overtones; (2) quasi-periodic spectrum with "energy exchange between normal modes which are strongly coupled by an internal resonance relationship" (Chaigne et al, 2005 p.403); (3) chaotic spectrum, where the energy excites many modes and the frequency relationships are too complex to perceive as pitch, but are perceived as broadband coloured noise.
Touzé explains the three stages in more technical terms (Touzé et al, 2010 p.234):
"For small amplitude values of the forcing, a periodic regime is at hand. When the excitation frequency is close to an eigenfrequency [resonant frequency], a linear resonance occurs, large-amplitude motions are more easily observable, resulting in the appearance of harmonics of the forcing frequency. For moderate amplitudes, a bifurcation occurs and a quasiperiodic regime is observed. This quasiperiodic state is characterized by the appearance of a number of distinct frequency peaks in the spectrum, each of them being an eigenmode of the structure. Moreover, these new frequency peaks can be grouped by two or three, and they present simple non-linear resonance relationships with the excitation frequency [9,7,10,8]. Hence, this transition is interpreted as a loss of stability of the first excited mode, in favour of a coupled regime, involving all the modes that share an internal resonance relationship with the excitation frequency, the injected energy being spread all over this specific set of modes."
As the spectrogram analysis below shows, there are clear bifurcations between these three states. The non-linearity of the system is demonstrated by the sudden jumps from one state to the next as the amplitude is linearly increased. There is a short audio example of the same spectrum, it moves quickly from linear sine-wave to multiphonic sound to chaotic/noisy sound. The second image below shows the spectrum of the two-cymbal system and its resonant frequency peaks. The third image shows the two-cymbal system again (red) but superimposed are the separate spectra of the individual cymbals measured on their own (blue & green). The two-cymbal system is presumably a composite of the resonances of the two individual cymbals, but made more complex by the interefernce of different and similar vibrational modes, causing some peaks to be inverted or cancelled out. Other peaks appear to move by a few hz, this may be due to change in mass of the system.
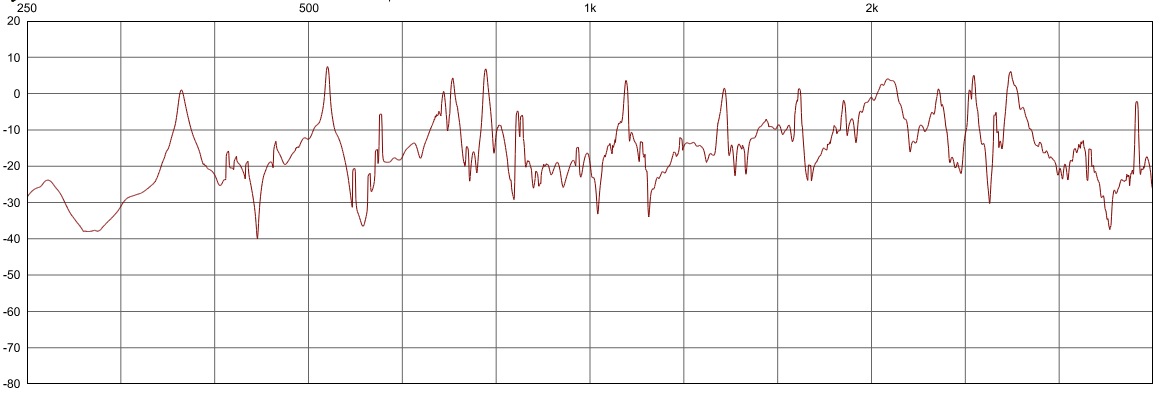
Cymbal spectrum
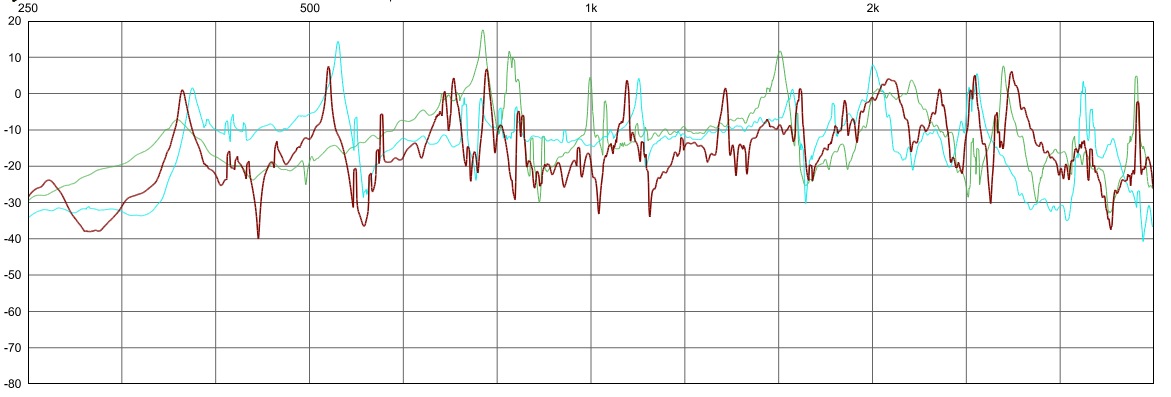
red = both, green+blue = the individual cymbals
Near Future
The next step for these pieces is simply to do more research on the performative aspects, become more fluent in the control of the instrument. I'll also be looking into the possibility of using MaxMSP to create a autoperformance system that listens to the cymbals and varies the input accordingly. The next big project will be to have several systems runnig together that talk to each other, different cymbals and different resonances searching for points of interaction.
References
Bidlack, R. (1990),
Music From Chaos: Nonlinear Dynamic Systems as Generators of Musical Materials, Dissertation UCSD,
www.ex-tempore.org/bidlack/bidlack.htm, accessed 21/5/2012.
Chaigne A., Touzé, C., Thomas, O. (2005), "Nonlinear vibrations and chaos in gongs and cymbals",
Acoust. Sci. & Tech. 26/5, 403-409.
Touzé, C., Thomas, O., Amabili, M. (2010), "Transition to chaotic vibrations for harmonically forced perfect and imperfect circular plates",
International Journal of Non-Linear Mechanics, 46 (2011) 234-246.







 Cymbal spectrum
Cymbal spectrum